Kardioit

Qırmızı əyri bir kardioitdir.

Kardioit — Yerin indiki forması (yəni qütblərdən basıq kürə).

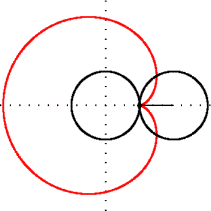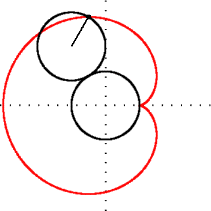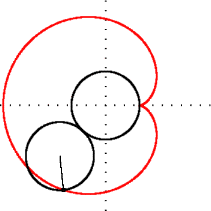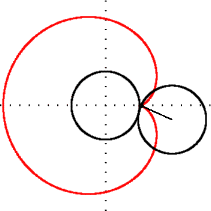
Riyaziyyatda kardioit və ya ürək əyrisi, sabit bir çevrə üzərində fırlanmasında olan eyni radiuslu ikinci çevrə üzərindəki hər hansı bir nöqtənin izlədiyi əyridir. Adı Yunanca kardia (ürək) və eidos (şəkil) sözlərinin birləşməsindən yaranmışdır. Ürək (♥) şəklinə bənzədiyinə görə belə adlandırılmışdı. Kardioit adını ilk dəfə 18-ci əsrdə yaşamış italyan riyaziyyatçısı Johann Castillon işlətmişdir.

Radiusu a olan iki çevrənin yaratdığı kardioit, Karteziyan koordinant sistemində bu tənliklə ifadə edilir:

$\,(x^{2}+y^{2}+ax)^{2}=a^{2}(x^{2}+y^{2}).$

Eyni bir əyri, 0 < t < 2π üçün bu parametrli tənliklərdə (iki dəyişənli tənliklər) də ifadə edilə bilər:

$\,x(t)=a\cos t(1-\cos t),$

$\,y(t)=a\sin t(1-\cos t).$

Qütb koordinat sistemində isə kardioitin ifadəsi belədir:

$\,r=a(1-\cos \theta ).$

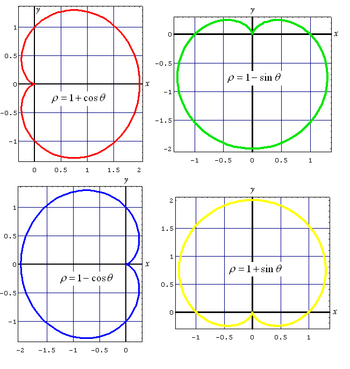
Triqonometrik funksiyaların bəzi çevirmə düsturları sayəsində, bu tənlikdə kosinus ifadəsini sinus ilə dəyişdirib, mənfi yerinə müsbət yazıla bilər. Ortaya çıxan şəkillər, eyni kardioitin mənşə ətrafında fırlanmış nüsxələri olacaqdır:

Kardioit, limaçon əyrisinin xüsusi bir nümunəsidir.

Sahə və çevrə

a radiuslu iki çevrənin yaratdığı kardioitin çevrə uzunluğu və sahəsi, qütb koordinatlarının köməyilə sadə yol ilə hesablanıla bilər:

$C=\int _{0}^{2\pi \,}{\sqrt {r^{2}+\left({\frac {dr}{d\theta }}\right)^{2}}}\,d\theta =\int _{0}^{2\pi \,}a{\sqrt {2-2\cos \theta }}\,d\theta =8a.$

$A=\int _{0}^{2\pi \,}\int _{0}^{a(1-\cos \theta )}r\,drd\theta ={\frac {a^{2}}{2}}\int _{0}^{2\pi }(1-\cos \theta )^{2}\,d\theta ={\frac {3}{2}}\pi a^{2}\,.$

Xarici keçidlər

• MacTutor riyaziyyat tarixi arxivindən Kardioit səhifəsi (İngilis dilində)
• MathWorld-dən Kardioit səhifəsi (İngilis dilində)