Romb

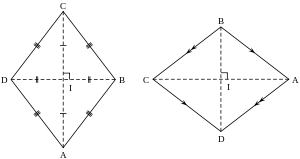
Romb (yun. ρομβος) — bütün tərəfləri bərabər olan paraleloqramdır. Bütün bucaqları düz bucaq olan romba kvadrat deyilir.

Rombun dioqanalları və tərəfi arasındakı əlaqə düsturu:

d1² + d2² = 4a²

Diaqonalları

• Diaqonalların uzunluqları fərqlidir;
• Diaqonallar kəsişmə nöqtəsində yarıya bölünür;
• Diaqonalları qarşılıqlı perpendikulyardır;
• Diaqonalı uyğun təpə nöqtələrində yerləşən bucaqların tənbölənidir;
• Hər bir diaqonalı rombu iki bərabəryanlı üçbucağa ayırır;
• Rombun dioqonalları düz bucaq altında kəsişir.

Xassələri

• Bütün tərəfləri bərabərdir.
• Qarşı tərəfləri bir-birinə paraleldir.
• Qarşı bucaqları bərabərdir.
• Birtərəfli bucaqlarının cəmi 180°-dir.

Perimetri

• $DC=a,CB=a,BA=a,AD=a\,$olduğundan P=4a. Eyni düstur kvadrat üçün də doğrudur.

Sahəsi

1)Rombun sahəsi diaqonallarının hasilinin yarısına bərabərdir.

2) Rombun sahəsi tərəfinin kvadratı ilə bu tərəflər arasında qalan bucağın sinusunun hasilinə bərabərdir.

$S_{ABCD}=a^{2}\cdot sin\alpha \,$

• ID = IB = d
• IC = IA = c

$S_{ABCD}=2{dc}\,$

3) Rombun sahəsi tərəfi ilə hündürlüyünün hasilinə bərabərdir.

S=ah

4)Rombun daxilinə çevrə çəkilərsə:

S=2ar