Ümumdünya cazibə qanunu
| Fəza-zaman |
|---|
 |
|
Xüsusi nisbilik Ümumi nisbilik |
|
Fəza-zaman konseptləri |
|
Klassik qravitasiya |
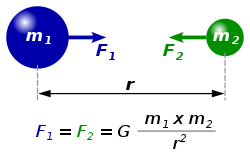
Ümumdünya cazibə qanunu — məşhur ingilis fiziki İsaak Nyutonun təklif etdiyi qanuna görə aralarındakı məsafə , kütlələri və olan iki maddi nöqtə bir- birini kütlələrinin hasili ilə düz,aralarındakı məsafənin kvadratı ilə tərs mütənasib olan qüvvə ilə cəzb edir:
Qravitasiya sabiti – kütlələri 1 kq, aralarındakı məsafə 1 metr olan iki bircins kürə arasındakı cazibə qüvvəsinə bərabər olan sabitdir, G= м³/(кq·san²). Qravitasiya sahəsinin əsas xassəsi budur: -Qravitasiya sahəsini mənbəyi kütlədir:böyük kütləli cisimlərin qravitasiya sahəsi kiçik kütləli cisimlərin qravitasiya sahəsinden daha böyükdür.Bilirik ki bütün cisimlər yer tərəfindən cazibə olunur.Həm də Günəş bütün planetləri həmçinin də Yeri cəzb edir.Buna səbəb Günəşin kütləsinin planetlərin kütləsinin hamısından böyük olmasıdır.Ümumdünya cazibə qanunu belə ifadə olunur:
Cazibə qüvvəsi cisimlərin kütlələri ilə düz,arasındakı məsafənin kvadratı ilə tərs asılıdır.
Nyutonun cazibə qanunun xüsusiyyətləri[redaktə | mənbəni redaktə et]
- Nyuton nəzəriyyəsinə görə hər konkret kütlə özünə cəzbetmə sahəsi yaradır, bu sahə qravitasiya sahəsi adlanır. Bu sahənin potensialı var və kütləli maddi nöqtə üçün qravitasiya potensialının funksiyası belə hesablanır:
- Ümumi halda ρ maddəsinin sıxlığı qaydasız yarananda, φ Puasson tənliуinə uyğun gəlir :
- Tənliyin həlli belə götürülür:
- r — dV həcminin elementi ilə φ potensialı hesablanan nöqtə arasındakıməsafədir. С — təxmini görtürülən məlum rəqəmdir.
- kütləli maddi nöqtənin qravirasiya sahəsinə təsir edən cəzbetmə qüvvəsinin hesablama tənliyi:
- Kürəvi simmetrik həcm həcmin mərkəzində yerləşən maddi nöqtə qədər cəzbetmə yaradır.
- Böyük kütləli həcm tərəfindən yaradılan qravitasiya sahəsindəki maddi nöqtənin trayektoriyası Kepler qanunu ilə hesablanır.
Tarixi arayış[redaktə | mənbəni redaktə et]
Ümüdünya cazibə qanunu ideyası Nyutona qədər də bir sıra görkəmli alimlər tərəfindən irəli sürülmüşdü. Bu barədə Epikür, Pyer Qassendi, İohan Kepler, Borelli, Rene Dekart, Roberval, Xristian Hüygens və başqaları öz fikirlərini bildirmişdilər. Kepler hesab edirdi ki, cazibə Günəşə qədər olan məsafəyə əks proporseonaldır; Dekart bildirirdi ki, cazibə fəzada olan küləklərin nəticəsidir. Düzgün fikirlər də rast gəlinirdi; Nyuton "Başlanğıc" əsərində özündən əvvəl bu mövzuya toxunan və düzgün nəticəyə gələn İsmael Bulliald, Rena Kristofer və Robert Hukun adını çəkir.[1] Buna baxmayaraq Nyutona qədər heç kim cəzbetmə qanununu və planetlərin hərəkəti qanununu( Kepler qanunu) onun qədər aydın və riyazi şəkildə izah edə bilməmişdi.
İ.Nyuton 1686 cı ildə özünün möhtəşəm Natural fəlsəfənin riyazi əsasları əsərində o dövrdə məlum olan emprik Kepler qanununa əsaslanaraq cəzbetmə qanununu hazırladı. O göstərdi ki:
- planetlərin hərəkəti isbat edir ki, mərkəzi qüvvə vardır ;
- mərkəzi cəzbetmə qüvvəsi elliptik orbit yaradır.
Nyutonun nəzəriyyəsinin əvvəlki alimlərin hipotezindən bir sıra kəskin fərqləri vardır. O tək formul təklif etməyərək, həm də aşağıdakı qanunların mükəmməl riyazi modelini işləyib hazırladı:
- cəzbetmə qanunu;
- hərəkət qanunu (Nyutonun ikinci qanunu);
- riyazi analiz.
Ümumilikdə bu üç qanun göy cisimlərinin mürəkkəb hərəkətini tədqiqatı üçün tam kifayət edir. Onun əsasında fəza mexanikası elmi yaradıldı. Albert Eynşteynə qədər bu modelə dəyişiklik edən olmadı. Baxmayaraq ki, modelin riyazi aparatına xeyli dəyişiklik etmək lazım gəlirdi.
Nyutonun nəzəriyyəsi heç də heliomərkəzçilik deyildi. Sonrakı tədqiqatlar göstərdi ki, planetlər Günəş ətrafında deyil, ümumi mərkəz ətrafında hərlənirlər. Belə ki, tək Günəş deyil, planetlər də Günəşi cəzb edir. Həmçinin planetlərin də bir – birinə təsirini nəzərdən qaçırmaq olmaz.
Müəyyən dövrdən sonra elmi arşdırmalar nəticəsində aydınlaşdı ki, ümumdünya cazibə qanunu ilə göy cisimlərinin hərəkətini dəqiqliklə hesablamaq olar.
Bununla belə bu qanunla bir sıra halları izah etmək olmur. Qanunun fiziki deyil, riyazi qanun olduğu hiss edilir. Beləki, cazibə qanunu hansı mexanizmlə planetlər arasındakı fəzanı keçir və o ani baş verir. Həmçinin kainat sonsuz və göy cisimləri arasında materiya yoxdursa, qravitasiya necə baş verir. Son dövrlərdə Merkurinin nəzəri və müşahidə yerdəyişmələri arasında müəyyən fərqlər vardır.
Nyutondan sonra iki yüz il ərzində fiziklər onun cəzbetmə qanunun təkmilləşdirilməsi üzərində çalışıblar. Bu ancaq 1915-ci ildə Albert Eynşteynin ümumi nisbilik nəzəriyyəsi yarandıqdan sonra mümkün oldu. Bununla da Nyuton nəzəriyyəsinin çətinlikləri özünə cavab tapdı. Aydın oldu ki, Nyuton nəzriyyəsi iki şərt daxilində mümkün olur:
- Tədqiqat sistemində qravitasiya potensialı düşünülən qədər çox deyil ( çox azdır ).
- Bu sistemdə hərəkət sürəti işıq sürətinin cüzi hissəsini təşkil edir.
Ədəbiyyat[redaktə | mənbəni redaktə et]
- Isaac Newton: "In experimental philosophy particular propositions are inferred from the phenomena and afterwards rendered general by induction": "Principia", Book 3, General Scholium, at p. 392 in Volume 2 of Andrew Motte's English translation published 1729.
İstinadlar[redaktə | mənbəni redaktə et]
- ↑ Xristian Hüygensə görə,dairəvi hərəkətdə mıərkəzəqaçan qüvvə (uyğundur) , burada — obyektin sürəti, — orbitin radiusu. Ancaq , burada — dövretmə periodu, belə ki . Keplerin 3-cü qanununa görə, , ona görə də , buna görə də son nəticə: .




















