Termodinamika
Termodinamika — makroskopik cisimlərin daxili durumunu tarazılıqda öyrənən elm. Başqa sözlə termodinamika qarşılıqlı çevrilmə və enerji ötürülməsini öyrənən elmdir.[1][2] Fizika elminin əsas bölmələrindən biridir.
Xarakteristika
[redaktə | mənbəni redaktə et]
Termodinamika enerjinin və qanunların bir növdən digərinə çevrilmələrini öyrənən elm sahəsidir. İşçi maddələrin köməyi ilə istilik və mexaniki enerjilərin qarşılıqlı çevrilməsinə baxılan hissəsi texniki termodinamika adlanır. Bir-biri ilə və ətraf mühitlə qarşılıqlı əlaqəsi olan cisimləri göstərən termodinamik sistem texniki termodinamikanın əsaslarından biridir. Termodinamik sistemlərə misal olaraq silindrdə porşenin hərəkəti ilə genişlənən və ya sıxılan qazları göstərmək olar.
Termodinamik sistem olan konkret fiziki şərtləri təyin etmək üçün para-metrlərin vəziyyəti adlanan göstəricilərdən istifadə olunur. Əsas parametrlərə temperatur T, təzyiq P və həcm V (və ya xüsusi həcmin əksi olan sıxlıq ρ) daxildir. Termodinamik sistemdə işçi maddənin vəziyyətinin dəyişmə ardıcıllığı termodinamik proses adlanır. Termodinamikada vahid sahəyə düşən qüvvəyə təzyiq deyilir. Termodinamikada qüvvə vahidi olaraq Nyuton (N), sahə vahidi isə metr kvadratı (m²) qəbul olunduğundan, təzyiq N/m² ilə ölçülür.
Təzyiq 2 yerə bölünür: mütləq və izafi təzyiqlər. Mütləq təzyiqdə işçi maddənin qabın daxilindəki həqiqi təzyiqi başa düşülür. İzafi təzyiqdə mütləq təzyiqlə ətraf mühit arasındakı təzyiqlər fərqi başa düşülür. Bu fərqləri ölçən cihaz manometr adlanır.
Qapalı qabda yerləşən qazın təzyiqi atmosfer təzyiqindən kiçik olarsa, belə qazın seyrəkliyini başqa sözlə vakuumunu manometrlə deyil, vakuummetrlə ölçmək lazım gəlir. Kiçik təzyiqləri ölçmək üçün içərisinə su, civə və ya digər maye doldurulmuş mayeli cihazlardan istifadə olunur.
Termodinamik faza
[redaktə | mənbəni redaktə et]Termodinamik faza, maddənin başqa hissələrindən kəskin sərhədlə ayrılan fiziki bircins hissəsinə deyilir.
Xarici şəraitdən (temperatur, təzyiq və b.) asılı olaraq maddə müxtəlif fazalarda ola bilər. Fazaların sayı aqreqat hallarının sayından çoxdur. Eyni bir aqreqat halında bir neçə faza ola bilər.
Fazalara misallar
[redaktə | mənbəni redaktə et]— Bərk, maye və qaz (məsələn, buz, su və su buxarı) ;
— Tərkibi eyni olub fərqli quruluşa malik olan kristallar (məsələn, almaz və qrafit) ;
— Normal və ifratkeçirici halda olan metallar;
— Paramaqnit və ferromaqnit;
— Paraelektrik və seqnetoelektrik və s.
Faza və komponent anlayışlarını fərqləndirmək lazımdır. Komponent – sistemin elə hissəsidir ki, onun tərkibi sistemin qalan hissələrinin tərkibindən asılı olmasın. Müxtəlif qazların qarışığı (müxtəlif qazlar istənilən nisbətdə tam qarışır) birfazalı, lakin çoxkomponentli sistemdir (komponentlərin sayı sistemdə olan müxtəlif qazların sayı qədərdir). Digər tərəfdən, su və onun üzərindəki su buxarı birlikdə ikifazalı, lakin birkomponentli sistemdir (hər iki faza eyni molekullarından ibarətdir).
Müəyyən şəraitdə maddə eyni zamanda iki və daha artıq fazada ola (yanaşı yaşaya) bilər. Məsələn, normal atmosfer təzyiqində () temperaturda buz və su; maye və onun üzərindəki buxar. Molekullar bir fazadan digərinə keçdiyinə görə bu fazaların hər biri açıq sistemdir. (Zərrəciklərin sayı dəyişməyən sistemlərə termodinamikada qapalı sistemlər, dəyişən sistemlərə isə açıq sistemlər deyilir.) Müəyyən şərtlər ödəndikdə bu açıq sistemlər tarazlığa gəlir.
Maddənin bərk və maye fazalarınn eyni zamanda yaşaya bildiyi tempertur ərimə temperaturu adlanır. Kristal cisimlərin ərimə temperaturu maddənin növündən başqa, təzyiqdən də asılıdır. Ərimə temperaturundan kiçik temperaturlarda məddə yalnız bərk, bundan böyük temperaturlada isə yalnız maye halında ola bilər.
Maye və onun üzərindəki buxar misalında fazaların tarazlığı üçün onların temperaturları (istilik tarazlığı şərti), təzyiqləri (mexaniki tarazlıq şərti) və bir fazadan digərinə və əksinə keçən molekulların sayı (maddi tarazlıq şərti) eyni olmalıdır.
Birkomponentli (eyni molekullardan ibarət) sistemin maye və ya qaz halında olması təkcə maddənin növündən və temperaturdan yox, həm də təzyiqdən asılıdır. Temperaturun hər bir qiymətinə uyğun elə bir təzyiq vardır ki, bu təzyiqdə maddə eyni zamanda həm maye, həm də qaz halında mövcud ola bilər.

Maddənin eyni zamanda həm maye, həm də qaz halında mövcud ola bildiyi hallar müstəvisində bir əyri ilə ifadə olunur (Şəkil 1-də AB əyrisi). Bu əyri fazaların tarazlıq əyrisi adlanır. Tarazlıq əyrisi müstəvisini iki hissəyə bölür. Əyrinin sol tərəfindəki hallarda yalnız maye faza, sağ tərəfindəki hallarda isə yalnız qaz fazası mümkündür. Tarazlıq əyrisi üzərindəki hallarda hər iki faza yanaşı yaşayır, yəni maye və qaz fazaları tarazlıqdadır. Əyri boyunca hərəkət etdikdə tarazlıq pozulmur, lakin maddənin müxtəlif fazalarının nisbi miqdarı dəyişir.
Əgər təzyiqin verilmiş qiymətində temperaturu artırmaqla (xaricdən istilik verməklə) sistemin halını dəyişdirsək sistem halından tarazlıq əyrisi ilə kəsişənə qədər bircins olaraq maye halında qalır, əyri üzərindəki nöqtəsinə uyğun olan halda sistem təbəqələşir, yeni faza-qaz fazası yaranır. Bu nöqtəyə uyğun halda sistemə xaricdən istilik verilməsinə baxmayaraq sistemin temperaturu dəyişmir, ona görə ki, verilən istilik mayeni buxara çevirməyə sərf olunur. Mayenin hamısı buxara çevrildikdən sonra buxarın temperaturu artır və sistem halına keçir.
Üçqat nöqtə
[redaktə | mənbəni redaktə et]Xüsusi şəraitdə maddənin üç aqreqat halı eyni zamanda tarazlıqda ola bilər. Bunun üçün hər üç fazanın temperaturu təzyiqi və kimyəvi potensialı eyni olmalıdır. Bu, təzyiq və temperaturun yalnız bir qiymətində mümkündür. (P, T) müstəvisində həmin nöqtə üçqat nöqtə adlanır (Şəkil 2-də O nöqtəsi). Buz, su və su buxarı üçün üçqat nöqtənin koordinatları: P0 = 0,006 atm , T0 = 273K [1].
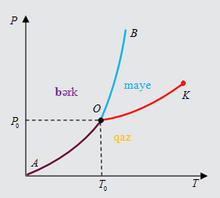
Üçqat nöqtədən kənar hallarda sistem yalnız bir fazada (bərk, maye və qaz) və ya iki fazanın tarazlığı halında olur. Cüt-cüt fazaların tarazlıq əyriləri olan AO (bərk-qaz), BO (bərk-maye) və KO (maye-qaz) əyriləri üçqat nöqtədə kəsişirlər.
Maye-qaz tarazlıq əyrisi (P, T) K nöqtəsində qurtarır. Bu nöqtəyə kritik (böhran) nöqtə deyilir. Kritik nöqtəyə uyğun kritik halda maye ilə onun buxarı arasında fərq yox olur.
Bərk-qaz və bərk-maye tarazlıq əyriləri üzərində isə kritik nöqtə müşahidə olunmur. Üçqat nöqtədən başlayan bərk-qaz tarazlıq əyrisi koordinat başlanğıcında qurtarır, bərk-maye tarazlıq əyrisi isə sonsuzluğa qədər uzanır.
Təzyiqin P< P0 qiymətlərində temperaturu artırdıqda bərk faza mayeyə çevrilmədən birbaşa qaz fazasına keçir. Bu hadisə sublimasiya, əks proses isə desublimasiya adlanır.
Maddənin bərk və maye fazalarınn eyni zamanda yaşaya bildiyi tempertur ərimə temperaturu adlanır. Kristal cisimlərin ərimə temperaturu maddənin növündən başqa, təzyiqdən də asılıdır. Verilmiş təzyiqdə ərimə temperaturundan kiçik temperaturlarda məddə yalnız bərk, bundan böyük temperaturlada isə yalnız maye halında ola bilər.
Təzyiqin P0< P< PK intervalında temperatur artarkən sistem ardıcıl olaraq hər üç fazadan keçir: bərk→maye→qaz.
Təzyiqin P> PK qiymətlərində temperaturu artırdıqda sistem OB əyrisini kəsərək bərk fazadan maye fazaya keçir, temperaturun T> T(0) qiymətlərində isə sistem OK əyrisini kəsmir-K nöqtəsindən yuxarıdan keçir (bu halda maye və qaz eyni zamanda mövcud olmur).
Faza keçidi(faza çevrilməsi)
[redaktə | mənbəni redaktə et]Xarici şəraitin (temperatur, təzyiq və b.) dəyişməsi nəticəsində maddənin bir termodinamik fazadan digərinə keçməsi faza keçidi (faza çevrilməsi) adlanır[1]. Faza keçidi zamanı maddənin halını xarakterizə edən kəmiyyətlərdən biri və ya bir neçəsi sıçrayışla dəyişir.
Bütün təcrübi faktları təhlil edərək Erenfest 1933-cü ildə faza keçidlərinin təsnifatını vermişdir. Bu təsnifata görə faza keçidləri iki növə bölünür: birinci və ikinci növ faza keçidi.
Birinci növ faza keçidləri elə keçidlərə deyilir ki, keçid nöqtəsində sistemin Gibbs termodinamik potensialı (və kimyəvi potensialı) kəsilməz, lakin bu potensialın birinci törəmələri ilə təyin olunan fiziki kəmiyyətlər (entropiya və həcm) sıçrayışla dəyişsin.
İkinci növ faza keçidləri elə keçidlərə deyilir ki, keçid nöqtəsində sistemin Gibbs termodinamik potensialı (kimyəvi potensial) və bu potensialın birinci törəmələri ilə təyin olunan fiziki kəmiyyətlər (entropiya və həcm) kəsilməz, lakin Gibbs potensialının ikiinci törəmələri ilə təyin olunan fiziki kəmiyyətlər (istilik tutrumu, sıxılma, istidən genişlənmə əmsalı) sıçrayışla dəyişsin.
Termodinamik potensiallar
[redaktə | mənbəni redaktə et]Termodinamik potensiallar (termodinamik funksiyalar) — termodinamik sistemin tarazlıq halı haqqında bütün məlumatları özündə saxlayan funksiyalardır. Termodinamik potensiallardan hər hansı birini bilməklə sistemə aid olan bütün termodinamik parametrləri və onlar arasında ümumi münasibətləri tapmaq olur.
Qapalı sistemin termodinamik potensialları
[redaktə | mənbəni redaktə et]Qapalı (zərrəciklərinin sayı dəyişməyən) sistemlərdə adətən 4 termodinamik potensial daxil edilir [1]: daxili enerji, entalpiya (istilik funksiyası), sərbəst enerji (Helmhols potensialı) və Gibbs potensialı.
Bu potensialların hamısının ölçüsü enerji vahididir. Onların mütləq qiyməti məlum olmur, yəni müəyyən sabit (bu sabit mütləq sıfırda daxili enerjinin qiymətidir) dəqiqliyi ilə tapılırlar. Lakin bu qeyri-müəyyənlik termodinamik parametlərin tapılmasına mane olmur, çünki bu parametrlər termodinamik potensialların dəyişməsi-onların birinci və ya ikinci tərtib xüsusi törəmələri kimi ifadə oluna bilir.
Termodinamik parametrlər-sistemin halını ifadə etməyə imkan verən kəmiyyətlərdir. Həcm (), entropiya (), təzyiq () və temperatur () termodinamik parametrlərdir.
Qapalı sistemin tarazlıq halında sistemə məxsus termodinamik potensialların hər biri 2 dəyişənin funksiyası kimi ifadə olunur. Bu sərbəst dəyişənlərə termodinamik potensialın təbii dəyişənləri deyilir.
Aydındır ki, termodinamik potensialların qiyməti sistemin termodinamik fazasından asılıdır.
Sistemin termodinamik parametrlərinin və onlar arasında ümumi münasibətlərin termodinamik potensiallar daxil etməklə öyrənilməsi metodu termodinamik potensiallar metodu adlanır.
Daxili enerji
[redaktə | mənbəni redaktə et]Cismlə bağlı hesablama sistemində onun bütün zərrəciklərinin hərəkəti və qarşılıqlı təsiri ilə bağlı olan bütün enerjilərin cəminə daxili enerji deyilir.
və -nin funksiyası kimi ifadə olunan daxili enerji termodinamik potensial adlanır, yəni temodinamik potensial kimi daxili enerjinin təbii dəyişənləri və -dir: . Daxili enerjinin dəyişməsi termodinamikanın birinci qanunu ilə müəyyən edilir:
.
Burada – sistem 1 halından 2 halına keçəndə daxili enerjisinin dəyişməsi, – bu prosesdə sistemin aldığı () və ya verdiyi () istilik miqdarı, sistem üzərində xarici qüvvələrin gördüyü işdir (sıxılmada , genişlənmədə ).
Qeyd edək ki, sistemin özünün gördüyü iş .
Diferensial şəkildə termodinamikanın birinci qanunu:
.
İzoxor () prosesdə iş görülmədiyi üçün sistemə verilən (alınan) istilik miqdarı onun daxili enerjisinin dəyişməsinə bərabər olur: .
və termodinamikanın ikinci qanununa görə olduğunu nəzərə aldıqda daxili enerjinin dəyişməsini diferensial formada belə yazmaq olar:
Sonuncu tənlikdən görünür ki, daxili enerjinin həcm və entropiyadan asılılığını bilsək digər iki parametri – temperatur və təzyiqi daxili enerjinin xüsusi törəmələri kimi hesablamaq olar:
, .
Mötərizənin aşağısında göstərilən kəmiyyət törəmə alınarkən sabit götürülür.
asılılığı təkcə və – nin deyil, istənilən digər termodinamik kəmiyyətlərin tapılmasına imkan yaradır. Məsələn, izoxor () prosesdə olduğu üçün, sabit həcmdə istilik tutumu daxili enerjinin törəməsi kimi aşağıdakı şəkildə ifadə olunur:
.
Entalpiya (İstilik funksiyası)
[redaktə | mənbəni redaktə et]Entalpiya, dəyişməsi izobar () prosesdə sistemə verilən (ondan alınan) istilik miqdarına bərabər olan kəmiyyətdir. Entalpiya
düsturu ilə təyin edilir. Buradan
. Bu ifadədə olduğunu nəzərə alsaq entalpiyanın dəyişməsi üçün
alarıq. Buradan alınır ki, termodinamik potensial olaraq entalpiyanın təbii dəyişənləri entropiya və təzyiqdir: .
Sonuncu tənlikdən görünür ki, entalpiyanın entropiya və təzyiqdən asılılığını bilsək digər iki parametri – temperatur və həcmi onun xüsusi törəmələri kimi tapmaq olar:
, .
asılılığı məlum olduqda istənilən termodinamik kəmiyyəti tapmaq olar. Məsələn, izobar () prosesdə olduğu üçün, sabit təzyiqdə istilik tutumu
.
Termodinamik potensial olaraq daxili enerji və entalpiya funksiyalarının əlverişli olmayan bir cəhəti var – onların təbii dəyişənlərindən biri təcrübədə birbaşa ölçülə bilməyən kəmiyyət olan entropiyadır. Ona görə də təbii dəyişənləri ölçülə bilən ,, parametrləri olan termodinamik potensiallar daxil edilir.
Sərbəst enerji (Helmhols potensialı)
[redaktə | mənbəni redaktə et]Sərbəst enerji, dəyişməsi izotermik () prosesdə görülən işə bərabər ola kəmiyyətdir. Başqa sözlə, sərbəst enerji daxili enerjinin işə çevrilə bilən hissəsidir.
Sərbəst enerji
düsturu ilə təyin edilir ( -ə bəzən bağlı enerji deyilir). Buradan . Bu ifadədə olduğunu nəzərə alsaq sərbəst enerjinin dəyişməsi üçün
alarıq. Buradan alınır ki, termodinamik potensial olaraq sərbəst enerjinin (Helmhols potensialının) təbii dəyişənləri həcm və temperaturdur: .
Sonuncu tənlikdən görünür ki, asılılığını bilsək digər iki parametri – təzyiq və entropiyanı onun xüsusi törəmələri kimi tapmaq olar:
, .
asılılığı məlum olduqda istənilən termodinamik kəmiyyəti tapmaq olar.
Gibbsin termodinamik potensialı
[redaktə | mənbəni redaktə et]işarə edək (bu ifadəni belə də yazmaq olar: . Onda
. Bu ifadədə yuxarıda alınmış münasibətini nəzərə alsaq:
.
Təbii dəyişənləri və olan funksiyası Gibbsin termodinamik potensialı adlanır. Termodinamik tədqiqatlarda Gibbs potensialından daha çox istifadə edilir. Bu, onunla bağlıdır ki, mürəkkəb sistemin tarazlıq halında Gibbs potensialının təbii dəyişənləri olan T və P sistemin hər yerində eyni olur.
Sonuncu tənlikdən görünür ki, funksiyasının açıq şəkliniı bilsək həcmi və entropiyanı tapa bilərik:
, .
asılılığı məlum olduqda istənilən termodinamik kəmiyyəti və termodinamik əmsalları tapmaq olar.
Sistemin makroskopik halını təyin edən parametrlərdən birinin dəyişməsinin digərini necə dəyişdiyini göstərən və təcrübədə ölçülə bilən kəmiyyətlərə termodinamik əmsallar deyilir.
İstilik tutumu (izoxor və izobar prosesdə istilik tutumu), təzyiqin izoxor termik əmsalı, izotermik sıxılma əmsalı və b. termodinamik əmsallardır.
Açıq sistemin termodinamik potensialları
[redaktə | mənbəni redaktə et]Zərrəciklərinin sayı dəyişməyən sistemlərə qapalı, dəyişən sistemlərə isə açıq sistemlər deyilir.
Məsələn, qapalı qabda olan maye və onun üzərində doymuş buxar bir yerdə qapalı sistemdir, lakin bu qabdakı maye (eləcə də buxar) açıq sistemdir: temperatur və ya həcm dəyişdikdə maye və buxar fazalarda olan molekulların sayı dəyişir.
Başqa misallar:
— bir-biri ilə kontaktda olan bərk və maye fazaların hər biri açıq sistemdir (sistemə istilik verdikdə fazalardakı molekulların sayı dəyişir);
— qapalı qabda qabın divarları ilə tarazlıqda olan foton qazı (divarın temperaturu dəyişdikdə fotonların sayı dəyişir);
— kristallarda fonon qazı (kristalın temperaturu dəyişdikdə fononların sayı dəyişir);
— yarımkeçiricilərdə keçirici zonada olan elektronlar, eləcə də valent zonada olan deşiklər (temperatur dəyişdikdə onların sayı dəyişir);
— kimyəvi reaksiyalar zamanı komponentlər (reaksiya prosesində hər bir komponentin zərrəciklərinin sayı dəyişir) və s.
Açıq sistemlərin termodinamik halı yuxarıda qeyd etdiyimiz dörd parametrdən (həcm — V, entropiya — S, təzyiq — P və temperatur — T) başqa, sistemdə olan zərrəciklərin sayı ilə təyin olunur. Ona görə də tarazlıq halında açıq sistemə məxsus termodinamik potensialların hər biri iki deyil, üç dəyişənin funksiyası kimi ifadə olunur: üçüncü dəyişən zərrəciklərin sayıdır.
Qeyd edək ki, yuxarıda tanış olduğumuz dörd termodinamik potensialın hamısı additiv kəmiyyətdir — onların qiyməti zərrəciklərin sayı ilə düz mütənasibdir [1,2]. Zərrəciklərinin sayı dəyişən sistemlərin halını təsvir etmək üçün kimyəvi potensial (μ) anlayışından istifadə edilir.
Kimyəvi potensial – iş görmədən sistemə bir zərrəcik əlavə edəndə sistemin enerjisinin dəyişməsinə bərabər olan kəmiyyətdir.
Sistemdəki zərrəciklərin sayı N qədər dəyişəndə onun enerjisinin dəyişməsi μN — ə bərabər olar, deməli, termodinamik potensialların yuxarıda verilmiş ifadələrinin hər birinə μN həddi əlavə olunmalıdır. Beləliklə, termodinamik potensialların diferensialları üçün yaza bilərik:
,
,
,
.
Bu ifadələrdən görünür ki, kimyəvi potensialı termodinamik funksiyaların hər birini -ə görə diferensiallamaqla tapmaq olar:
Qeyd edək ki, müxtəlif hallarda kimyəvi potensial müxtəlif parametrlərin funksiyası olacaq. Məsələn, termodinamik potensial olaraq Gibbsin termodinamik potensialını götürsək, yalnız temperatur () və təzyiqin () funksiyasıdır və zərrəciklərin sayından () asılı deyil.
Böyük termodinamik potensial
[redaktə | mənbəni redaktə et]Açıq sistemlərdə daha bir termodinamik potensial daxil edilir. bərabərliyində olduğunu nəzərə alsaq: .
Diferensialı
ifadəsi ilə təyin olunan
funksiyasına böyük termodinamik potensial və ya omeqa-potensial deyilir. Bu funksiyanın təbii dəyişənləri , və -dür: . Bu funksiyanın açıq şəklini bilsək, zərrəciklərin sayını, təzyiqi, entropiyanı və s. tapa bilərik:
; ; .
Sistemə mexaniki təzyiq qüvvəsindən fərqli xarici qüvvələr təsir etdikdə, bu təsirlərə məxsus enerjiləri () də böyük termodinamik potensiala əlavə etmək lazımdır. Əgər açıq sistem xarici elektrik sahəsində olarsa, , maqnit sahəsində olarsa, . Bu ifadələrdə – xarici elektrik sahəsinin intensivliyi, – bu elektrik sahəsinin təsiri ilə mühitdə yaranmış polyarizasiya vektoru, – xarici maqnit sahəsinin intensivliyi, – maqnit sahəsinin təsiri ilə mühitdə yaranan maqnitləşmə vektorudur.
Termodinamik əmsallar
[redaktə | mənbəni redaktə et]Termodinamik əmsallar, sistemin makroskopik halını təyin edən parametrlərdən birinin dəyişməsinin digər parametrləri necə dəyişdiyini göstərən və təcrübədə ölçülə bilən kəmiyyətlərə deyilir. İstilik tutumu (izoxor və izobar prosesdə istilik tutumu), təzyiqin izoxor termik əmsalı, izotermik sıxılma əmsalı və b. termodinamik əmsallardır.
İstilik tutumu
[redaktə | mənbəni redaktə et]Ədədi qiymətcə, sistemin (maddənin) temperaturunu bir dərəcə dəyişmək üçün lazım olan istilik miqdarına bərabər olan kəmiyyətə istilik tutumu deyilir [1].
Xüsusi istilik tutumu və molyar istilik tutumu anlayışlarından da istifadə edilir.
Bir kq (bir mol) maddənin temperaturunu bir dərəcə dəyişmək üçün lazım olan istilik miqdarına bərabər olan kəmiyyətə xüsusi (molyar) istilik tutumu deyilir.
İstilik tutumunu iki şəraitdə — izoxor () və izobar () şəraitdə ölçürlər.
İzoxor istililik tutumu : .
İzobar istililik tutumu: .
Burada -istilik miqdarı, -temperaturdur.
Həcmin istidən genişlənmə əmsalı
[redaktə | mənbəni redaktə et]Ədədi qiymətcə, sistemin temperaturunu bir dərəcə dəyişdikdə onun vahid həcminin dəyişməsinə bərabər olan kəmiyyətə həcmin istidən genişlənmə əmsalı deyilir.
Bu əmsalı iki şəraitdə — izobar () və adiobat () şəraitdə ölçürlər.
Həcmin istidən izobar genişlənmə əmsalı : .
Həcmin istidən adiobat genişlənmə əmsalı : .
Burada -entropiyadır.
Təzyiqin termik əmsalı
[redaktə | mənbəni redaktə et]Ədədi qiymətcə, sistemin temperaturunu bir dərəcə dəyişdikdə onun təzyiqinin nisbi dəyişməsinə bərabər olan kəmiyyətə təzyiqin termik əmsalı deyilir.
Bu əmsalı iki şəraitdə — izoxor () və adiobat () şəraitdə ölçürlər.
Təzyiqin izoxor termik əmsalı: .
Təzyiqin adiobat termik əmsalı: .
Sıxılma əmsalı
[redaktə | mənbəni redaktə et]Ədədi qiymətcə, sistemdə təzyiqi bir vahid dəyişdikdə onun vahid həcminin dəyişməsinə bərabər olan kəmiyyətə sıxılma əmsalı deyilir.
Bu əmsalı iki şəraitdə — izotermik () və adiobat () şəraitdə ölçürlər.
İzotermik sıxılma əmsalı: .
Adiobat sıxılma əmsalı:.
Sıxılma əmsalının tərsi həcm modulu və ya statistik modul adlanır [1] :
, .
Makroskopik parametrlər kimi termodinamik əmsallar da termodinamik potensiallar metodu ilə hesablana bilər [1,2]. Bu əmsallar termodinamik potensialların ikinci tərtib törəmələri ilə ifadə olunur:
; ; ;
; .
Burada -sərbəst enerji , isə Gibbsin termodinamik potensialıdır.
İstinadlar
[redaktə | mənbəni redaktə et]Ədəbiyyat
[redaktə | mənbəni redaktə et]- B. M. Əsgərov. Termodinamika və statistik fizika. Bakı, 2005, 631 səh.
- Базаров. Термодинамика. Санкт-Петербург — Москва — Краснодар, 2010, 376 стр.


































































































